Looking at the analog synthesizers of the 1970s, one thing immediately caught my eye: the absence of a sine wave in the waveform selector.
For me, the sine wave is the default waveform, and yet it is not present in the old synths. Why?
I discovered that there are two reasons. The first reason is that generating a sine wave with an analog circuit is not easy. It is straightforward to transition an analog signal from one level to another quickly to create a square wave. It is also easy to transition a signal from one level to another linearly to create a triangular or sawtooth wave. But transitioning a signal from 0 to 1 in the shape of a sine wave is complex.
Complex, but not impossible, so why not include it in the synths of a certain level?
Because the sine wave is not an interesting waveform for an analog subtractive synthesis-based synth, which was the case for most synths in the 1970s.
Let's dive a bit into the technical details.
An analog subtractive synthesizer relies on the idea that a certain waveform (or a combination of various waveforms) creates a number of harmonics that can be removed (subtracted) using an analog filter.
Square, sawtooth, and triangular waves all have a series of harmonics. To see a harmonic, you can apply the Fourier transform and switch from the time domain to the frequency domain, or you can use Ableton Live's Spectrum to see the frequency harmonics more simply.
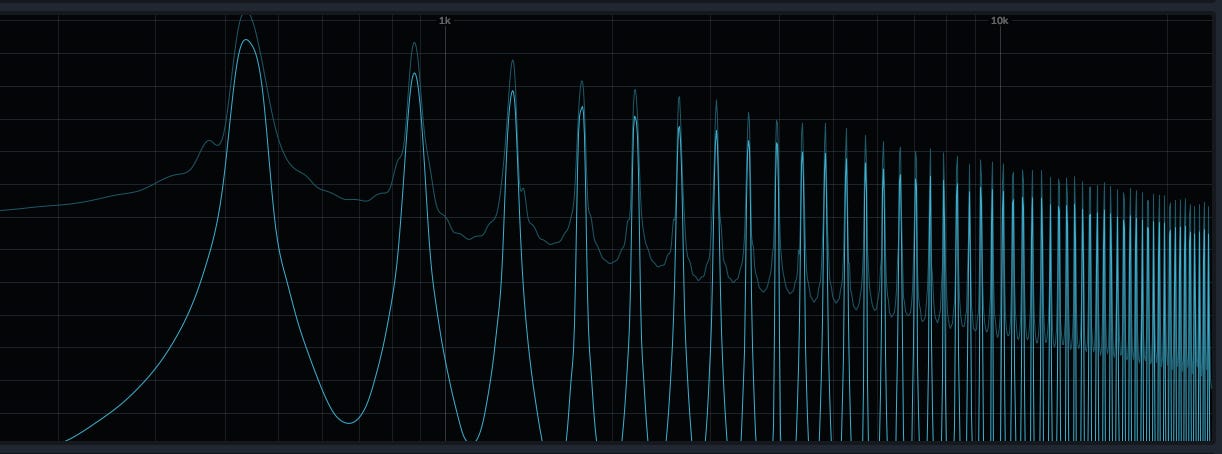
Take a sawtooth wave, the most common and richest in harmonics. Its spectrum (as it is called) looks like this:
The first peak is the fundamental frequency (f0), for example, the classical A with 440Hz. It is also the most significant peak and the most audible. Following that, there are other peaks at frequencies like 880Hz (f0 * 2), 1320Hz (f0 * 3), etc., with decreasing amplitudes (mathematically, the amplitude of the second harmonic is half of the fundamental, the third is 1/3, and so on).
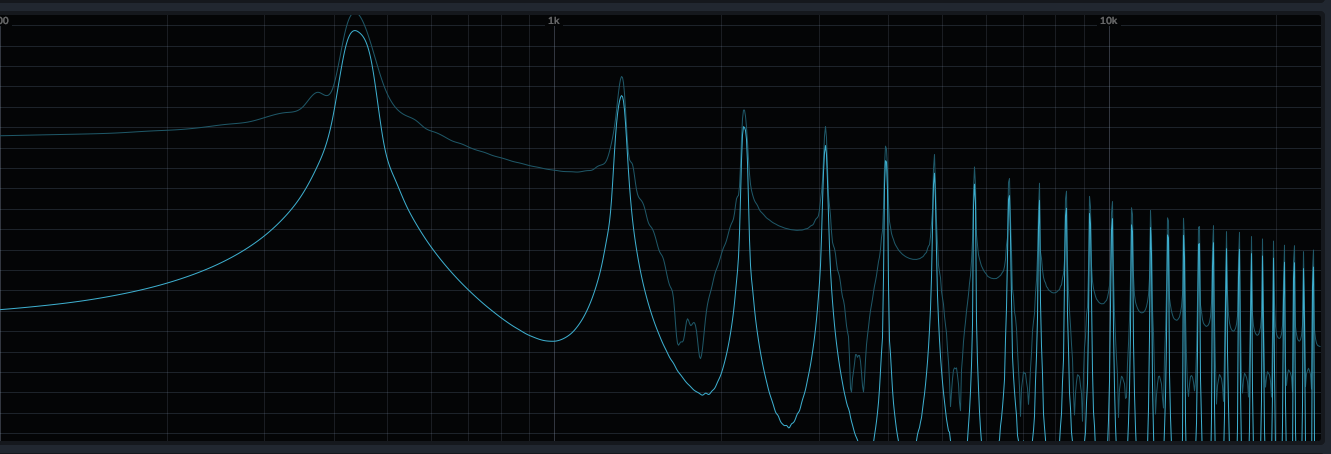
If we consider a square wave, there are fewer harmonics. Starting from the fundamental frequency f0, we will only have f0 * 3, f0 * 5, f0 * 7 (only the odd harmonics), and their amplitudes decrease inversely: 1/n (so 1/3, 1/5, 1/7, ...)
Even the triangular wave has the same harmonics as the square wave, but their amplitudes decrease with the square of the position 1/n^2: 1/9, 1/25, 1/49.
This rapid decrease in amplitude means that the harmonics are less audible, and indeed, the sound of the triangular wave is smoother than the others.
In subtractive synthesis, the final sound is created by removing harmonics from the waveform produced by the oscillators to achieve that classic synth effect found in bands like Pink Floyd or Emerson, Lake & Palmer.
Okay, but what does all this have to do with the sine wave?
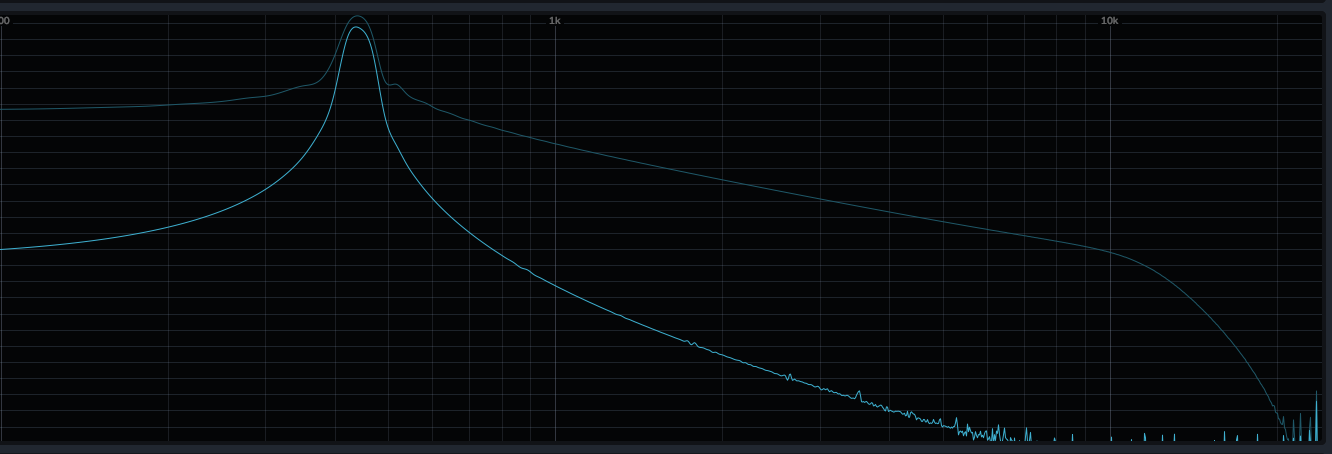
To understand that, just look at the spectrum of a sine wave to realize how little interest it arouses:
The sine wave has only one harmonic, the fundamental f0. It is a pure sound (and that's its beauty), but it is not very interesting for an analog subtractive synthesizer because there is nothing to subtract.
That's why synth manufacturers did not invest time in reproducing it in their instruments since their interest is limited in the case of subtractive synthesis.
This doesn't mean sine waves are not used; on the contrary, they are widely used in additive synthesis and also in frequency modulation (like the legendary DX7) to create the sounds that characterized the 1980s.
But we'll talk about that another time...